Introduction

Here is what we have done so far with our hockey players’ data set:

Part1: Calculated the means and create a normal distribution;

Part 2: Calculated the standard deviation;

Part 3: Found the correlation between height and weight; and

Part 4: Drew samples form the population and calculated their standard error.

In this post, we will include the NBA data set. We will compare the samples means of our hockey players vs our basketball players. Then we will attempt to categorize a random sample to the hockey or the NBA data set. That means if we blindly draw one player from the two data sets, we can establish ......or more importantly reject, from which data set that player came from.  We can even tie a statistic to it.

Sample means

We will draw the sample means for our basketball players as we did for our hockey players.

Height

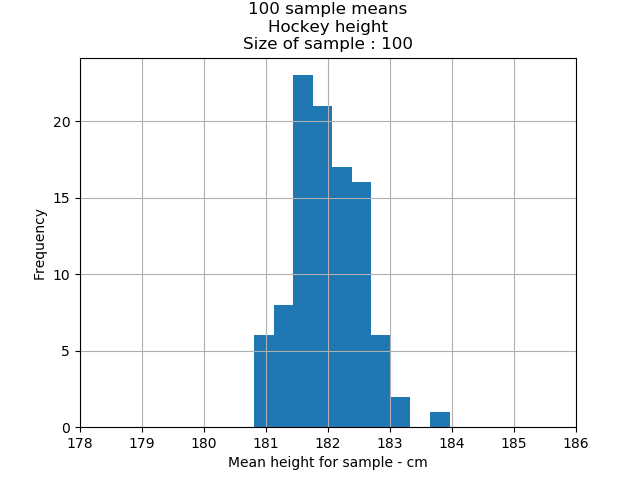
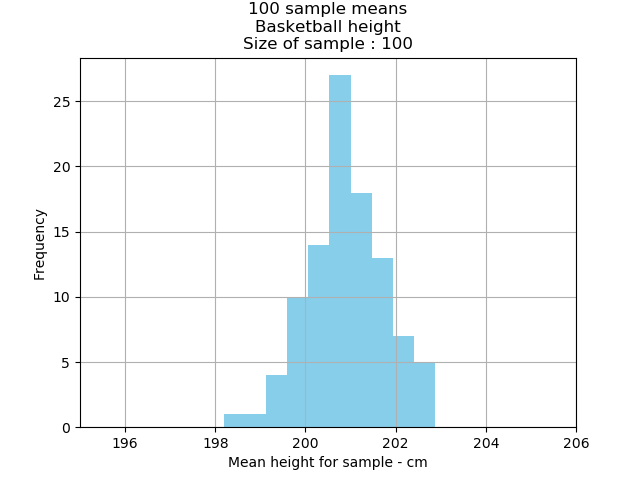
Hockey players’ height mean:                                    182.04cm

Hockey players’ height standard error:                      0.587

1 standard error: 68 percent of all sample means are between 181.45cm and 182.63cm;

2 standard errors: 95 percent of the sample means are between 180.87.cm and 183.21cm; and

3 standard error: 99.7 percent of the sample means are between 180.28cm and 183.80cm.

Basketball players’ height mean:                                200.81cm

Basketball players’ height standard error:                 0.919

1 standard error: 68 percent of all sample means are between 199.89cm and 201.73cm;

2 standard errors: 95 percent of the sample means are between 198.97.cm and 202.65cm; and

3 standard error: 99.7 percent of the sample means are between 198.053cm and 203.57cm.

Say we randomly draw a player with a height of 199.55cm from the two data sets. How can we accurately establish from which dataset this player was drawn or not drawn? We can use our frequency distribution of sample means.

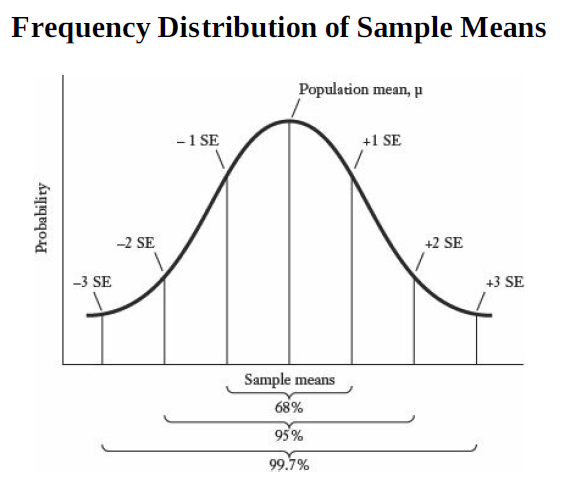
You can reject with a 99.7% confidence level that the randomly drawn player is NOT part of the hockey players’ data set. Why? Because a height of 199.55cm is more than 3 standard errors away from the population mean of the hockey players' data set.

Weight

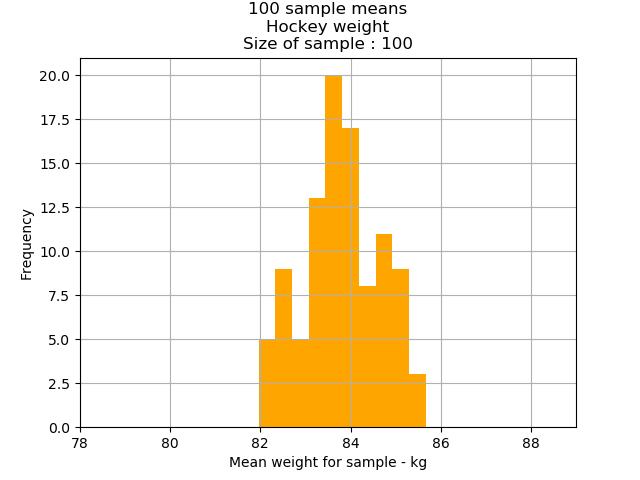
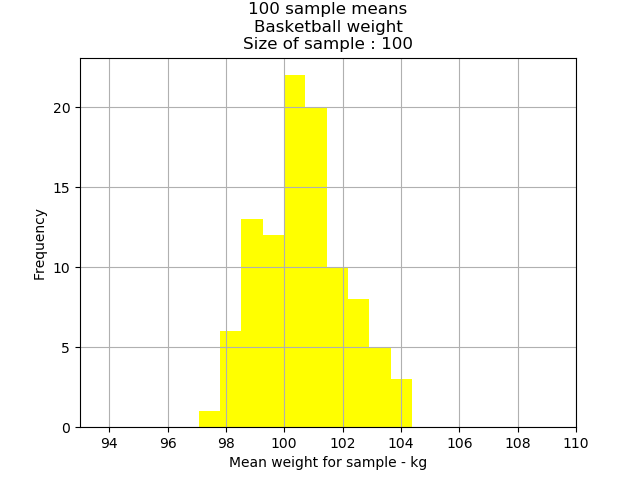
Hockey players’ weight mean:                                               83.74kg

Hockey players’ weight standard error:                                 0.855

1 standard error: 68 percent of all sample means are between 82.89kg and 84.60kg;

2 standard errors: 95 percent of the sample means are between 82.03.kg and 85.45kg; and

3 standard error: 99.7 percent of the sample means are between 81.18kg and 86.31kg.

Basketball players’ weight mean:                                           200.81cm

Basketball players’ weight standard error:                            0.919

1 standard error: 68 percent of all sample means are between 99.38kg and 101.90kg;

2 standard errors: 95 percent of the sample means are between 98.12g and 103.16kg; and

3 standard error: 99.7 percent of the sample means are between 96.87kg and 104.14kg.

Say we randomly draw a player weighing 81kg from the two data sets. How can we accurately establish from which dataset this player was drawn or not drawn?

You can reject with a 99.7% confidence level that the randomly drawn player is NOT part of the basketball players’ data set. Why? Because a weight of 81kg is more than 3 standard errors away from the population mean of the basketball players’ data set.

Conclusion

It is extremely unlikely that a sample mean will lie 3 or more standard erros from the population mean. That's all for now and I'll see you next time.

‍